Systolic Array Processor 2D
Hallo, in this part, i am trying to explain about systolic array processor, we can find this material in every VLSI books. The reference for this article is the book of Keshab K. Parhi “VLSI for Digital Signal Processing”. It is said that the systolic is just like the heart rate, it flows through the clock of processor. let choose a case of matrices multiplication.
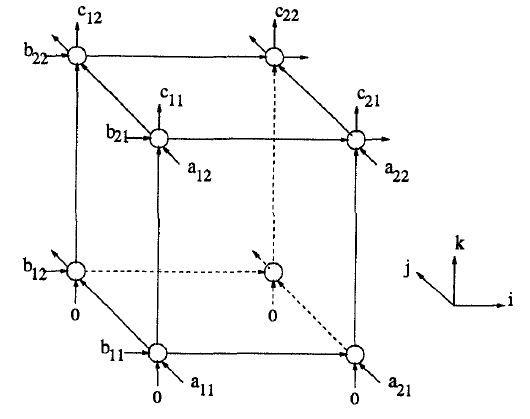
there will be four inputs, firs we need to draw the state space representation, shown on figure below
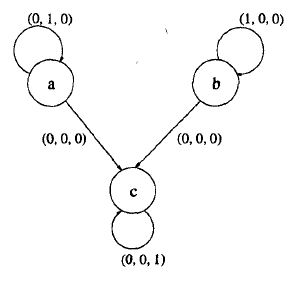
based on state representations, we see if the points A flow through axis J, B flow through axis i, and C at axis K. at every node there will be multiplication and the last node will be addiction process. we can see, the value of B changed at i direction, A at j direction, and C at the end of K direction. then we can draw the scheduling of reduce space representation shown bellow.
as we can see (i,j,k), a flows through j axis, b at i axis and c at k axis. there is no connection between A -> C or B -> C, so its labelled as (0,0,0). now we can calculate scheduling solution at matice S =(S1,S2,S3). since there no communication time between node, so Tcom = 0. then
Tcommunication between a to a >> 0, b to b >> 0, c to c >> 1, coz C is the output
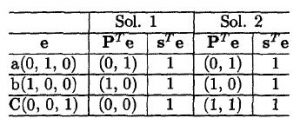
then the multiple solutions of matrices multiplication is
for (S1,S2,S3) is (1,1,1), d as projection vector, and P is Processor space vector, and S is scheduling vector. then we need to multiply the matrices between P (transpose) and matices d. the result must be orthogonal, and the calculation between S(transpose) and matrices d must be larger than zero. then we should mutiply this matrices with the edge mapping
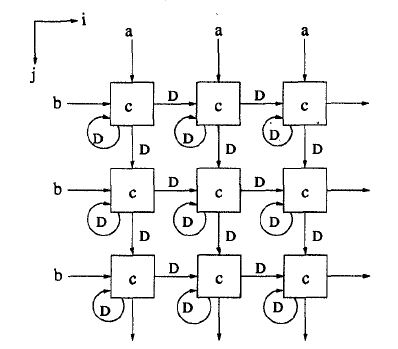
we can see at the table of solution 1, the matrices P(transpose) multiplied with the edge. we can draw then the two dimensional of systolic array as seen at figure bellow
from the 2D systolic state representation, C or the output stays at the node, and value of B are moving through i axis, and values of A moving through j axis.
source:
Keshab K Parhi “VLSI for Digital Signal Processing”

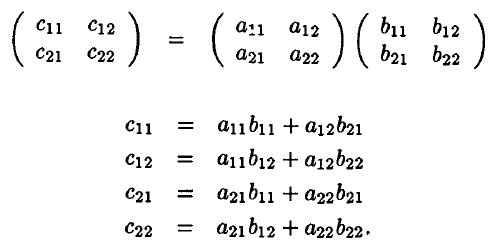
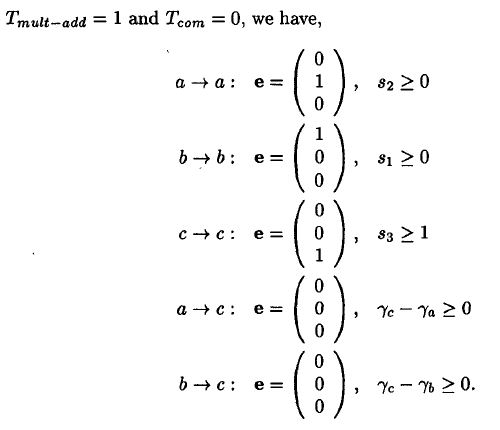
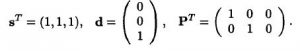
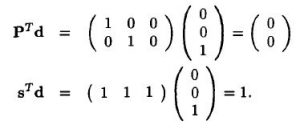
Recent Comments